どうもこたにんです。
穴だらけの筆算問題を解いてみた
同僚から「こういうのやる気出る?」というメッセージとともにこんな画像が届いた。
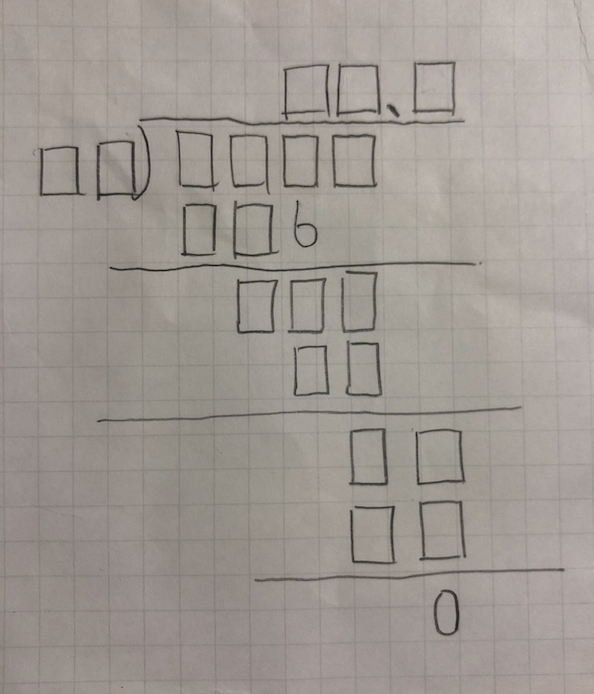
うん!!そそるね!!
見た瞬間に脳汁飛び出すよね!!!
ゾクゾクしてくるね!!
さて、この下には早速答えが貼ってあります。
ので、自力で解きたい方は、スクロールするのを躊躇ってください。
解答
仕事帰りの電車の中でさくっと解かせていただきました。
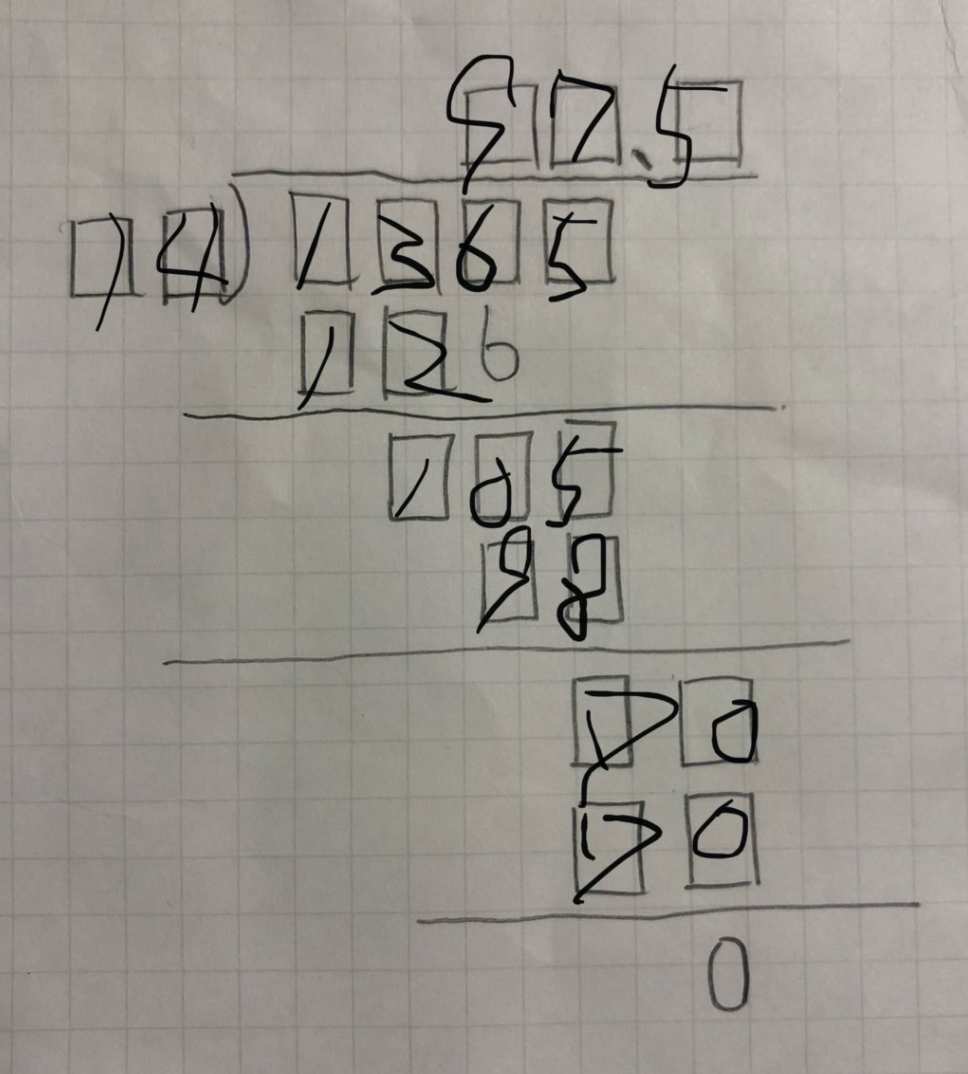
とても脳汁な問題だったので、わたしの解法を備忘しておきます。
解法
0. それっぽい条件を書き出してみる
まず問題の空欄をじーっと眺めて、いくつかの条件があることを見つけます。
- 割る数・商のどちらかは31より大きくなること(1000の平方根以上)
- 3桁−2桁のところは100台かつ差分が10未満であること
- 割る数の一の位と商の小数点第一位の組み合わせは、偶数×5 であること
- 最後に引き算される2桁は素数ではないこと
- 割る数の一の位は0ではないこと
実際に解きすすめるにあたって必要かどうかは置いておいて、これくらい。
闇雲にあてはめても答えは導けないので、きっかけを探します。
1. 割る数の一の位と小数点第一位を確定させる
一番わかり易いきっかけは、これでした。
- 割る数の一の位と商の小数点第一位の組み合わせは、偶数×5 であること
なぜこうなるのかというと、割り算の決まりを逆に考えればわかります。
割り算というのは [割られる数] ÷ [割る数] = [商] です。
逆に考えると、[割る数] × [商] = [割られる数] となります。
自明なのですが、今回の問題においては、この考え方が重要になります。
今回の問題は、商が整数ではなく小数点を持ちます。
が、割られる数は整数です。
それ即ち、[割る数] × [商] が 整数になる(小数点第一位が0になる)ということです。
そうすると、割る数の一の位と商の小数点第一位の組み合わせは以下4通りのみ。
(2, 5)(4, 5)(6, 5)(8, 5)
なので、小数点第一位が取りうる値は、上記の5つの数字のどれか、ということになります。
ここで問題をよーく見ます。
最初に割り算をする段、ここの一の位に 6 が最初から入っています。
ということは、割る数の一の位に 5 が入ることはありえません。
なので必然的に「小数点第一位=5」が確定します。
続いて、筆算の最終段に着目します。
最終段は、割る数と小数点第一位を掛け算した値が2桁である、という条件です。
ということは、割る数×5が3桁になってはいけない、ということ。
つまり、割る数が20以上になってはいけない、ということ。
なので必然的に「割る数の十の位=1」が確定します。
2. 割る数を確定させる
現段階で、割る数は4パターンに絞られました。
12, 14, 16, 18 のいずれかです。
さらに最初に割り算をする段に戻ると、割る数に何かを掛けて3桁になる必要があります。
しかも、下1桁が6になる必要がある。
12, 14, 16, 18 それぞれの数字で、条件を満たすのは以下です。
- 12:該当なし
- 14:14×9=126
- 16:該当なし
- 18:18×7=126
2択ですが、実は真ん中の割り算の段、ここが肝なのです。
- 3桁−2桁のところは100台かつ差分が10未満であること
これ、何を言っているかいいますと。
3桁の方が 100〜108、2桁の方が 91〜99 という数値しか取ることができないのです。
では、14 or 18 に何かを掛け算したときに、91〜99に収まる数字はあるでしょうか。
14×7=98、14×8=112、18×5=90、18×6=108
14×7のパターンしか、これを満たしません。
ということは、割る数が14でないといけないことがわかります。
ので、14×9=126と14×7=98を選ぶ必要があります。
なので必然的に「割る数=14」「商の整数部=97」が確定します。
3. あとは計算して埋める
割る数=14、商=97.5が確定しました。
あとはこれを下から埋めていくだけで全てのマスが埋まります。
以上。
楽しい問題をありがとう。
あとから聞いたら、Twitterから拾ってきた問題だったようです。
良問でした。
中一の弟作。
— あつと (@aty_carbuncle) 2020年2月3日
穴だらけながら答えが1つに定まる良問です。やるやん pic.twitter.com/s0jChgVuK1