どうもこたにんです。
「クーポンコレクター問題」を知って収集癖を数学的に分析しよう!

みなさん一度は、コンプリートする要素のあるものに触れたことはあるかと思います。
チョコエッグのような運で集めていく食玩とか、トレーディングカードとか、今どきで言えばソシャゲのコンプガチャとか。
たくさん買えばいつかコンプリートできるようなもの。
運とお金任せで集めていくのも楽しみ方のひとつなのでいいことです。
ただそれは、確率論を知れば、数学的に認識できるのです。
これは「クーポンコレクター問題」と呼ばれる確率論の問題です。
日本においては「食玩問題」と呼ばれています、名は体を表しますね。
クーポンコレクター問題って?
実はWikipediaの記事よりもニコニコ大百科の方が厚みがある記事になっています。
コレクターな人=オタク気質、というのは自明なのでニコニコの方が記事になっているのでしょうね。
冒頭の説明文も、すごくわかりやすいです。
ガチャガチャやお菓子つきのおもちゃ、アイドルCDの生写真など等確率でランダムに封入されているものについて、どのくらい買えば全種類手に入れられるかをあらかじめ見当付けたい時に役に立つ。
ね?
全種類集めたい!がいくらかかるかわからない!
といったときに役立つ数学が、クーポンコレクター問題なのです。
クーポンコレクター問題における期待値、すなわち全種類コンプするための期待値は以下の式で求められます。(Wikipediaより)
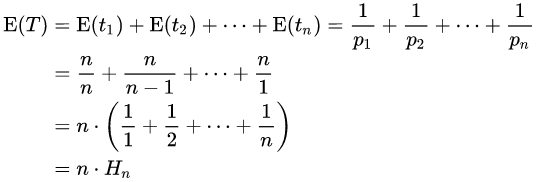
ここからは、ニコニコ大百科に記載されている事例などを交えてクーポンコレクター問題を体に染み込ませましょう。
ケース0:コインを振って表裏どちらも出るまでに振り続ける平均回数
上の式を理解するための入門として、一番簡単な例からいきます。
表裏の2面あるコインを何回振れば表も裏もどっちも出るか、そのときの期待値です。
ゴールは「表も裏も出ること」です。
- 1面目:1回振れば必ずどっちかが出る(厳密に言えば 2/2 の確率の逆数)
- 2面目:1回目で出た面じゃない面が出る確率は 1/2 、なので逆数の 2回 が期待値
これを足し算することで「表も裏も出る期待値」となります、1+2=3回です。
(足し算していいのは「期待値の線形性」という性質があるからです)
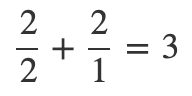
簡単に言うと、確率の逆数が期待値なのでそれを足し合わせようというわけです。
期待値なので必ずその回数ではないです、あくまでも期待値なので。
以後これを覚えておくこと。
ケース1:6面サイコロの目が全部出揃うまでに振り続ける平均回数
先のコインの場合と同じ考えをします、6パターンに増やします。
1面目は6面中6面なので6/6、2面目は6面中5面なので6/5、、、となります。
式に表すとこうなります。
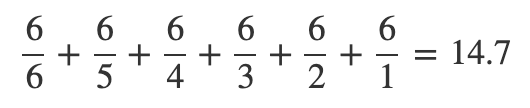
それぞれの目が出うる確率の逆数を足し合わせる、答えは14.7です。
なので、14.7回サイコロを振れば、たいてい6面全部出しきれるというわけです。
上の式は括るとこうなります。
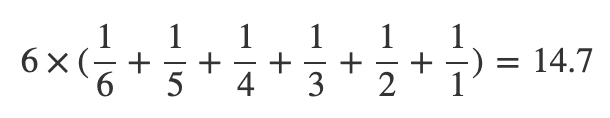
括ると、冒頭に示した一般式と同じ形になっていることがわかりますね。
ケース2:20種類の食玩をコンプするまでの平均回数
これは全部で20種類です、コンプまで時間がかかりそうです。

これも同様に、式に当てはめてやりましょう。
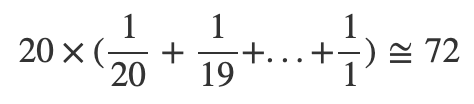
72回買えば揃いそうです。
このチョコエッグは1個200円なので、14,400円くらいで揃いますね。
全種類セットがメルカリで14,400円以下で売られていたらお得、ということです。
期待値から金額感を知り、転売の効果を見出すことまでできちゃうわけです。
数学って素敵ですね。
クーポンコレクター期待値早見表
上記ケースで期待値の算出方法はわかりました。
ただ、クーポンコレクター問題を適用したいケースって多いと思います。
たとえば今ハマっているどうぶつの森においても、収集要素が多いです。
いろんなケースをふまえ、ざっくり期待値早見表を作ってみました。
|
種類 |
期待値 |
期待値/種類 |
|
10 |
29.3 |
2.93 |
|
20 |
72.0 |
3.60 |
|
30 |
119.9 |
4.00 |
|
40 |
171.1 |
4.28 |
|
50 |
225.0 |
4.50 |
|
60 |
280.8 |
4.68 |
|
70 |
338.3 |
4.83 |
|
80 |
397.2 |
4.97 |
|
90 |
457.4 |
5.08 |
|
100 |
518.7 |
5.19 |
10種類コンプの期待値は29.3、20種類は72、30種類は119.9。。。
上記をだーいたいでならすとこんな感じの式になるかな。

種類数が増えるほど、4 の部分が大きくはなりますが。
だいたいざっくりこれくらいの計算式でおおよその期待値、としてもいいかもですね。
以上。
「クーポンコレクター問題」を知って収集癖を数学的に分析しよう、でした。
これでみんなも収集マスターだ!!
それでは聴いてください。