どうもこたにんです。
理系ホイホイなタイトルに見えて、実は誰でもホイホイな内容だったり。
はい、目次どん!
微分とは
微分とは - Google 検索
数学で習うやつですね、好き嫌いが大きく分かれるやつ。
極限を求めるやつ。
様々な分野で応用される、ザ・数学って感じの考え方のひとつ。
しかし今回は数学的なお話ではなく、それを日常に適用してみるというお話。
微分するということを「速度」を例に説明します
微分とは数学的に言えば、次元を下げるという働きをします。
線(2次元)を微分すると、点(1次元)になります。
グラフを用いてわかりみの良い表現をします。
例えば以下のようなふらふらしたグラフがあったとします。
上がったり下がったり、とてもふらふらしたグラフです。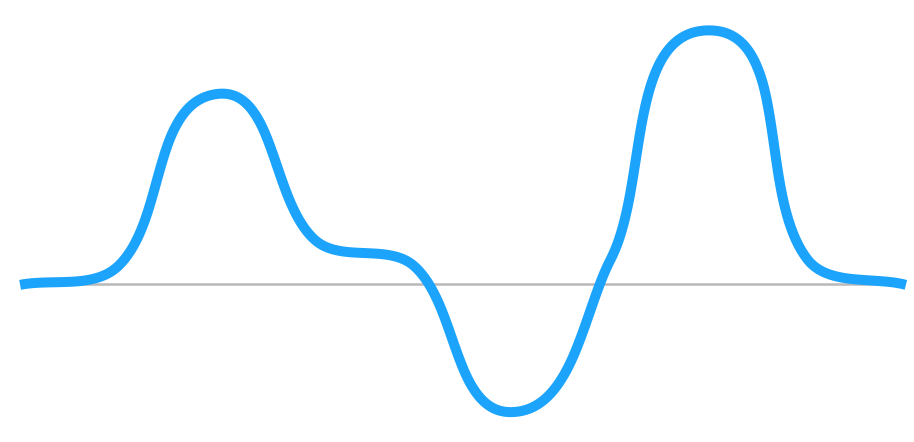
これを微分するとどういうことになるのかというと、ある程度誇張して図示。
伝わりが良いように、このグラフは車の速度を意味しているものとします。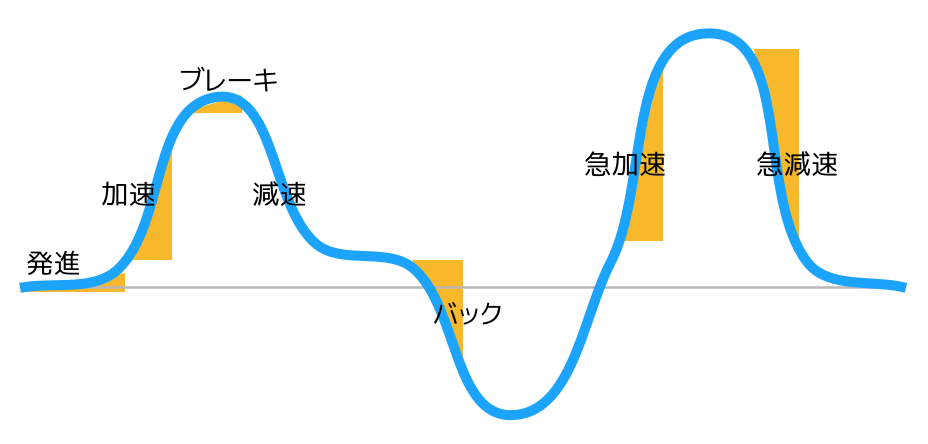
オレンジ色で表現した部分が微分、それすなわちを表現しています。
横軸を時間と捉えたときに、ある一定の時間内でどれくらいの速度を出したか、です。
最初は緩やかに発進して、途中から加速。
このときは初速は緩やかな速度だが、途中で大きな速度になる。
山でブレーキをかけて速度がゼロになり、そこから緩やかに落ちていく。
バックすると負の向きに速度が上がる。
後半で急加速し、ピークを迎えて、急減速する。
これは時間単位の変化量、その時間でどれくらいの速度の変化があったのか。
それを定数化できるのが、微分の性質です。
本来の微分は、このある一定の時間内を極限まで狭めます。
極限まで狭めることで、ある瞬間の速度を出すことができる。
微分するということを「こたにん」を例に説明します
席に座って首を振りたい気分のこたにんがいたとします。
そんな謎の行動を取ろうとしているこたにんを、連写するとどうなるか。



止まっているこたにん、首を振り始めたこたにん、首を激しく降るこたにん。
これが微分です。
ある地点、ある瞬間の、こたにんの変化量です。
残像がすごく激しいほど、そのときの運動量が多いということです。
(我ながら猛烈にいい例えを思い付いて表現できたが、何か大事なものを失った気がした)
微分するということを「アピール」を例に説明します
今一度このグラフをご覧ください。
ただし今回は波形に車という意味をもたせません。
青線の波形は、誰かが喋っているときの盛り上がり、と捉えてみてください。
誰かが何かを語ってアピールしている場面を想定してみる。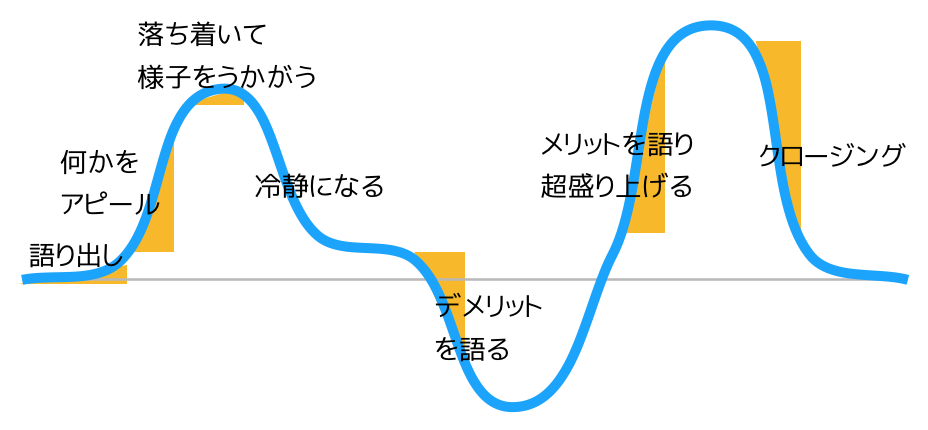
最初は緩やかに語り出してアピール。
このときはアイスブレイクしつつ緩やかに語り出し、途中で盛り上げていく。
一旦周囲を伺い、リアクションを見て、間を作りながら冷静に話す。
デメリットを語って、最後への布石とする。
後半でメリットを語り超盛り上げて、ピークを迎えて、クロージングする。
アピールの変化を微分するとこのようになります。
微分することで、そのときそのときに何を思っているのかが論理的にわかる。
そういった例でした。
言動を微分する
本項が本記事のピークかつまとめです、微分するとゼロになる点です。
変化量の増減を意識して伝え方を変える
上に示したグラフのように、変化量が増減するような話し方は伝わりが良いです。
テンションの上がり下がりのない平坦な説明では伝えきれない思いなどが伝わりやすい。
ただ上げるだけではなく、ときには下げつつ、場の雰囲気を伺いながら緩急をつける。
またそのときに、ボディランゲージなどのアクションが伴っているとさらに面白い。
一挙手一投足までもを微分して、変化を捉えると、もっと伝わり方が変わるかもしれないです。
変化量が高ければよいということではない
しかし、ただ変化量が高いだけではいけないです。
ときには平坦なグラフになるように、論理的に冷静に話すことも大事。
さらにもっと言うと、沈黙というスキルを使うとよいです。
沈黙には、ただ黙っている以上の効果を場にもたらします。
(沈黙についてで別記事書くことを今ここにコミットします)
数学は実生活に役に立つ
言いたいことはここ。
数学って、学生時代に習っているときは、数字を扱う学問として習う。
これって役に立つの?日常生活で微分とか解の公式とか三角関数とか使うの?
たしかに、数字を扱う仕事をしていない以上、役に立つシーンはそうそうないかもしれない。
だけど今回のように、数学の考え方をベースに、言動や過ごし方に適用できます。
微分だけではなく、他のいろんな数学知識を、生活に適用していくと面白いです。
そこから逆に、数学に興味を持ちましょう!
なぞの締めの言葉になってしまいました、別に数学者でもないんだけどね。
それでは。